- [[レビュー]]
- 試験 ?
- 課題 ★★★☆☆
- 秋山裕先生
- なんとテキスト科目のテキストをそのまま使用するという、非常にリーズナブルな授業。単位も半分と、テキスト統計学の短縮版と思われる。データの読み方から、正規分布~中心極限定理~[[仮説検定]]~回帰分析まで。excelの使い方を詳細に解説してくれており、神excelの使い手に一歩近づける。
- 以下では講義のまとめをします
-
第9回 [[仮説検定]]
- 仮説検定では分布の変化を評価し、主張の検証を行う
- 主張が統計学的にデータから支持されるかどうかを検証する
- [[仮説検定]]の手続き
- 仮説の設定
- 帰無仮説(H0:μ=65)が正しいとして分布を考え、得られた標本の平均(xb=70)がその分布の中で発生しにくいかどうかを考える。発生しにくければ対立仮説を支持する。#br
帰無仮説を正しいと考えるのは、対立仮説(H1:μ>65)を証明するのが大変だから。 - 帰無仮説に基づく分布の決定
- 標本の平均、標準偏差から、[[中心極限定理]]に基づき標本平均の分布を計算する。平均=標本の平均、標準偏差=標本の標準偏差/√n
- 検定統計量は[[標準化]]して[[標準正規分布]]にする。
- [[有意水準]]の決定
- [[有意水準]]とは、得られた標本平均が分布の中で「発生しにくい」と判断する確率のこと
- 社会科学では一般に5%が用いられる。
- [[棄却域]]の設定
- [[有意水準]]の領域の範囲を求めることを[[棄却域]]の設定という。
- 例えば対立仮説が「先学期の平均65点より高い」であれば、得られた標本平均が発生しにくいほど大きいければ対立仮説が支持されるので、[[棄却域]]は分布の右端になる。
- 有意水準が大きければ、[[棄却域]]も大きい
- [[標準化]]後なら、「z>NORM.S.INV(1-有意水準)」 が[[棄却域]]となる
- [[有意水準]]の領域の範囲を求めることを[[棄却域]]の設定という。
- 検定の結論
- 計算した検定統計量が[[棄却域]]に入っていれば「発生しにくい量」であると示されたことになる
- 発生しにくいことが起こったならば
- [[帰無仮説]]は棄却、[[対立仮説]]を採択
- 「有意水準?%で対立仮説が起こった」と結論できる
- [[棄却域]]に入っていなければ、[[帰無仮説]]を採択することになる([[対立仮説]]を棄却する、とは言わない)
- 平均に関する検定における標準正規分布と[[t分布]]
- 母集団の標準偏差が分からない場合は、標本の標準偏差で代用しなければならないが、[[標準正規分布]]を用いることができないので、代わりに[[t分布]]を使う
- 統計量が正規分布に従うと仮定しないといけない
- [[棄却域]]は「T.INV(有意水準,n-1)」で求められる
- 母集団の標準偏差が分からない場合は、標本の標準偏差で代用しなければならないが、[[標準正規分布]]を用いることができないので、代わりに[[t分布]]を使う
- [[P値]]による検定
- 計算した検定統計量よりも大きく(小さく)なる確率を[[P値]]という
- [[P値]]が[[有意水準]]より小さければ[[対立仮説]]を採択、大きければ[[帰無仮説]]を採択し、結論できる
- 具体的には 右片側検定なら「1-NORM.S.DIST(標準化した検定統計量)」 左片側検定なら「1-T.DIST(標準化した検定統計量)」が有意水準より小さいかどうかで判断すればいい
- 割合に関する検定
- 仮説の設定を H0:p=0.5, H1:p>0.5 のように行って同様に計算する
- 検定統計量は[[区間推定]]で計算したように z=(pt-p)/√(p(1-p)/n) で計算する。
- 同様に「1-NORM.S.DIST(標準化した検定統計量)」「1-T.DIST(標準化した検定統計量)」が有意水準より小さいかどうかで判断
- 例)n=300人に対してx=171人がA候補者に投票した場合
- 得票率pt=57% より z=2.42487, NORM.S.DIST(z,true)=0.99234より p(z > 2.42487) = 0.00766 よって[[有意水準]]1%でA候補は当選確実である
- [[第I種の過誤]]、[[第II種の過誤]]
- 仮説検定による結論は誤りである場合がある
- [[第I種の過誤]]は、帰無仮説H0が正しいのに棄却してしまう誤り。
- [[第II種の過誤]]は、対立仮説H1が正しいのに、帰無仮説H0を採択してしまう誤り。
- いずれも、結論と事実が棄却域の反対側にある場合に起きる誤りのこと。
- 過誤をなくすためには、有意水準を小さくしてやればいい
- 仮説検定では分布の変化を評価し、主張の検証を行う
-
第10回 相関分析
- 変化が起こったとき、なぜその変化が起こったのかを明らかにする
- [[散布図]]
- 2つの変数の関係を視覚的にとらえられる
- [[Excel]]では「挿入」「グラフ」「散布図」で作成可能
- [[共分散]]
- 関係の方向と関係の強さを数値で表現したもの
- 右上がりならプラス、右下がりならマイナス、関係が強ければ絶対値大、関係が弱ければ絶対値小
- 平均を軸として考える
- 第1象限・第3象限に各点が散らばっていれば正の相関
- 第2象限・第4象限に散らばっていれば負の相関
- 傾向がみられなければ各象限に散らばる
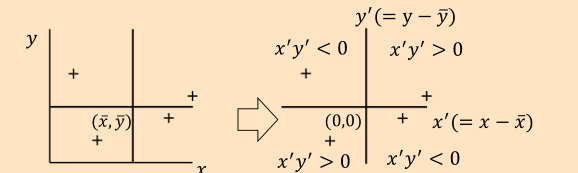
- ↑共分散でなぜ$$(x-\overline{x})(y-\overline{y})$$の平均を求めるのか、の理由
- [[Excel]]ではCOVARIANCE.Sを使って求める
- 値は単位の二乗になり、プラスマイナスくらいしか判断できないので、[[相関係数]]を使うことが多い
- [[相関係数]]
z_{x_i} = \frac{x_i-\overline{x}}{s_x}のように変換して[[標準化]]する。- 標準化した変数は単位なしになる。
z_xとz_yの[[共分散]]cov_{z_xz_y}を使って、相関係数ρ_{xy}は次のように表せる。-
ρ_{xy} = \frac{cov_{z_xz_y}}{s_xs_y} - 必ず-1~1の間になるので扱いやすい
- [[Excel]]ではCORRELで求められる
- みせかけの相関
- アイスクリームとビールの消費量のように、共通するほかの変数(気温z)が影響している場合でも[[相関係数]]は大きくなる
- 鵜呑みにしてはだめ
- [[相関係数]]と線形
- 相関係数は線形関係の強さを数値化したもので、非線形の関係の分析はできない
y=x^2の相関係数は0
- [[順位相関係数]]
- 極端に離れた値があると相関係数が大きく変わる(分布の歪み)
- 歪んだ分布についての尺度として、[[順位相関係数]]がある
- xとyのそれぞれを順位付けし、順位について相関係数を求める
- [[Excel]]ではRANK.AVGを使って求める
- 株と相関係数
- [[相関係数]]がマイナスとなる株を組み合わせると、[[標準偏差]]が非常に小さくなり、リスク回避ができる
-
第11回 [[回帰分析]]・[[最小二乗法]]
- [[相関係数]]からは、2つの変数に関係があることはわかるが、原因と結果の関係性が分からない
- [[回帰分析]]によって、2つの変数の関係を示す式を推定する
y = \alpha + \beta xy :被説明変数x :説明変数\alpha :回帰係数:定数項・切片\beta :回帰係数:傾き・勾配- 変数が1つの場合は単純回帰(単回帰)という。複数の場合は重回帰という。
- [[誤差]]
- [[誤差]]は縦方向に測る。誤差を
u_iとするとy_i = α + βx_i + u_i - 推定式を
\hat{y_i} = \hat{α} + \hat{β}x_iとすると、誤差をe_iとしてy_i = \hat{α} + \hat{β}x_i + e_iと表せる
- [[誤差]]は縦方向に測る。誤差を
- [[最小二乗法]]
y_i = \hat{α} + \hat{β}x_i + e_iの誤差e_iの2乗の和を最小にするように\hat{α}と\hat{β}を求める- 誤差
e_i = y_i - (\hat{α} + \hat{β}x_i)の2乗の和をとって偏微分 = 0を解くと\hat{\beta} = \frac{\sum(x_i - \bar{x})(y_i - \bar{y})}{\sum(x_i - \bar{x})^2}\hat{\alpha} = \bar{y} - \beta \hat{x}
- [[Excel]]では SLOPE と INTERCEPT で求められる。[[散布図]]→近似曲線の追加 でもできる。
- [[標準誤差]]
- [[誤差]]が小さければ信頼度が高く、誤差が大きければ信頼度が低い
- 標準誤差
s = \sqrt{\frac{1}{n-2}\sum_{i=1}^{n} e_i^2}- n-2で割るのは、実質的なデータの数がn-2だから。n=1では直線が引けず、n=2だと誤差が0になる。
- √をとるのは単位をそろえるため。
- [[Excel]]では STEYX を使って求める。
- 標準誤差は見ただけでは何を表しているのかよくわからないので、[[決定係数]]が広く利用されている
- [[決定係数]]
\sum e_i^2 = \sum (y_i - \bar{y})^2 - \sum (\hat{y}_i -\bar{y})^2- $$y_i$$ : 実績値、 $$\hat{y}_i$$ : 回帰分析による理論値
- 移項して $$\sum (y_i – \bar{y})^2 = \sum (\hat{y}_i -\bar{y})^2 + \sum e_i^2$$
- 全平方和 = 回帰による平方和 + 残差平方和
- 信頼度が高いとき、回帰の平方和:大、残差平方和:小
- 信頼度が低いとき、回帰の平方和:小、残差平方和:大
- [[決定係数]]は全平方和に対する回帰による平方和の比率で表す。
- $$r^2 = \frac{\sum_{i=1}^{n}(\hat{y}i – \bar{y})^2}{\sum{i=1}^{n}(y_i – \bar{y})^2}$$
- 必ず0~1の間になる。0なら説明していない、1なら完全に説明している。
- 相関係数の2乗と等しい
- [[Excel]]では RSQ で求める
- 回帰分析という名前はゴルトン(1822-1911)によるもの。因果分析という名称の方が適切。
-
第12回 [[回帰分析]]・[[信頼区間の推定]]と[[仮説検定]]
- 回帰分析で得られた直線の信頼度は[[決定係数]] $$r^2$$ の大きさだけではわかりにくい
- [[最小二乗法]]で推定した式 $$y = \hat{\alpha} + \hat{\beta}x $$ の $$\hat{\alpha}$$ と $$\hat{\beta}$$ の分布を考える
- $$\hat{\alpha}$$ と $$\hat{\beta}$$ の散らばりが大きければ信頼できないし、散らばりが小さければ信頼できる
- 標本n個を抽出するごとに$$\hat{\alpha}$$ と $$\hat{\beta}$$が1つ決まる。そこで、[[中心極限定理]] で $$\hat{\beta}$$ の分布を考える
- $$\hat{\beta}$$ の分布
- いくつかの仮定が成立するとき、 $$y = \alpha + \beta x + u $$ の母集団から大きさ n の標本を抽出したときの回帰係数 $$\hat{\beta}$$ は 平均 $$\beta$$、標準偏差 $$s{\hat{\beta}} = \frac{s}{\sum{i=1}^{n} (xi – \bar{x})^2}$$ の分布に従い、$$t = \frac{\hat{\beta} – \beta}{s{\hat{\beta}}}$$ は 自由度 n-2 の [[t分布]]に従う。
- 5つの仮定:誤差に偏りがない、誤差同士に関係がない、誤差の平均の大きさは一定、説明変数と誤さに関係がない、誤差が正規分布に従う(要するに、誤差がランダムの時にだけ成立する)
- 古典的[[最小二乗法]]という
- いくつかの仮定が成立するとき、 $$y = \alpha + \beta x + u $$ の母集団から大きさ n の標本を抽出したときの回帰係数 $$\hat{\beta}$$ は 平均 $$\beta$$、標準偏差 $$s{\hat{\beta}} = \frac{s}{\sum{i=1}^{n} (xi – \bar{x})^2}$$ の分布に従い、$$t = \frac{\hat{\beta} – \beta}{s{\hat{\beta}}}$$ は 自由度 n-2 の [[t分布]]に従う。
- $$\hat{\beta}$$ の[[信頼区間の推定]]
- [[t分布]]について$$-t{\alpha /2}~t{\alpha /2}$$ に $$(1-\alpha) * 100(%)$$の領域を考える
- $$P(\hat{\beta} – t{\alpha /2} s{\hat{\beta}} < \beta < \hat{\beta} + t{\alpha /2} s{\hat{\beta}} ) = 1 – \alpha$$ という形になる。
- Excelでは、T.INV(1-α/2, n-2) で $$t{\alpha/2}$$を求め、sは STEYX 、$$\sum{i=1}^{n} (xi – \bar{x})^2$$は DEVSQ で求めて割り、 $$s{\hat{\beta}}$$ を求める。
- LINEST 関数で回帰分析に必要な様々な値を求められる。計算結果を置く範囲指定後にCtrl+Shift+Returnを押す
- [[t分布]]について$$-t{\alpha /2}~t{\alpha /2}$$ に $$(1-\alpha) * 100(%)$$の領域を考える
- $$β$$ の[[仮説検定]]
- tが[[自由度]] n-2 の[[t分布]]に従うことを利用して仮説検定を行える
- $$y = \alpha + \beta x$$ の $$\beta$$ の検定については、次の仮説に関する検定([[有意性検定]])が広く行われている
- $$H_0 : \beta = 0$$ (xが消え、yの大きさの決定にxが有意でなくなる)
- $$H_1 : \beta \neq 0$$ (yの大きさの決定にxが有意である)
- 帰無仮説$$H_0$$が正しいときに標本データから求めた$$\hat{\beta}$$が発生しにくいと判断する領域は、プラスとマイナス側の両方になる。tでも同様。
- [[有意水準]]5%、n=4なら、T.INV(0.975,2) = 4.303より、棄却域はt > 4.303とt < -4.303 となる
- 検定統計量 $$t = \frac{\hat{\beta} – \beta}{s_{\hat{\beta}}} (\beta = 0)$$ が[[棄却域]]に入った→帰無仮説が発生しにくい→帰無仮説を棄却、対立仮説を支持(棄却域に入れば影響ありと判断する)
- [[P値]]による[[仮説検定]]
- 検定統計量 $$t = \frac{\hat{\beta} – \beta}{s_{\hat{\beta}}}$$ を計算し、*T.DIST(t, n-2, true) 2** が有意水準より小さければ[[帰無仮説]]棄却
- T.DISTに2をかけるのは両端に棄却域があるから
- 検定統計量 $$t = \frac{\hat{\beta} – \beta}{s_{\hat{\beta}}}$$ を計算し、*T.DIST(t, n-2, true) 2** が有意水準より小さければ[[帰無仮説]]棄却
